Collaborative Filtering Part 1: Memory-based Methods
by Yifei Zhou
1. Introduction
As I mentioned in the last blog, collaborative filtering is a popular algorithm in recommender systems. This type of method makes automatic predictions about a user's interests by collecting and comparing preferences information from many users. The underlying assumption of the collaborative filtering approach is that if person A has the same opinion as person B on an item, A is more likely to have B's opinion on a different item than that of a randomly selected person.
2. Memory-based methods
Memory-based methods, also called neighbor-based methods, build a user-item co-rated matrix from the database, where each entry within the matrix represents the rating item given by the user. Each row of the matrix can be viewed as a user vector representing a user's historical rating behaviour. Each matrix column can be seen as an item vector representing the users rated the item.
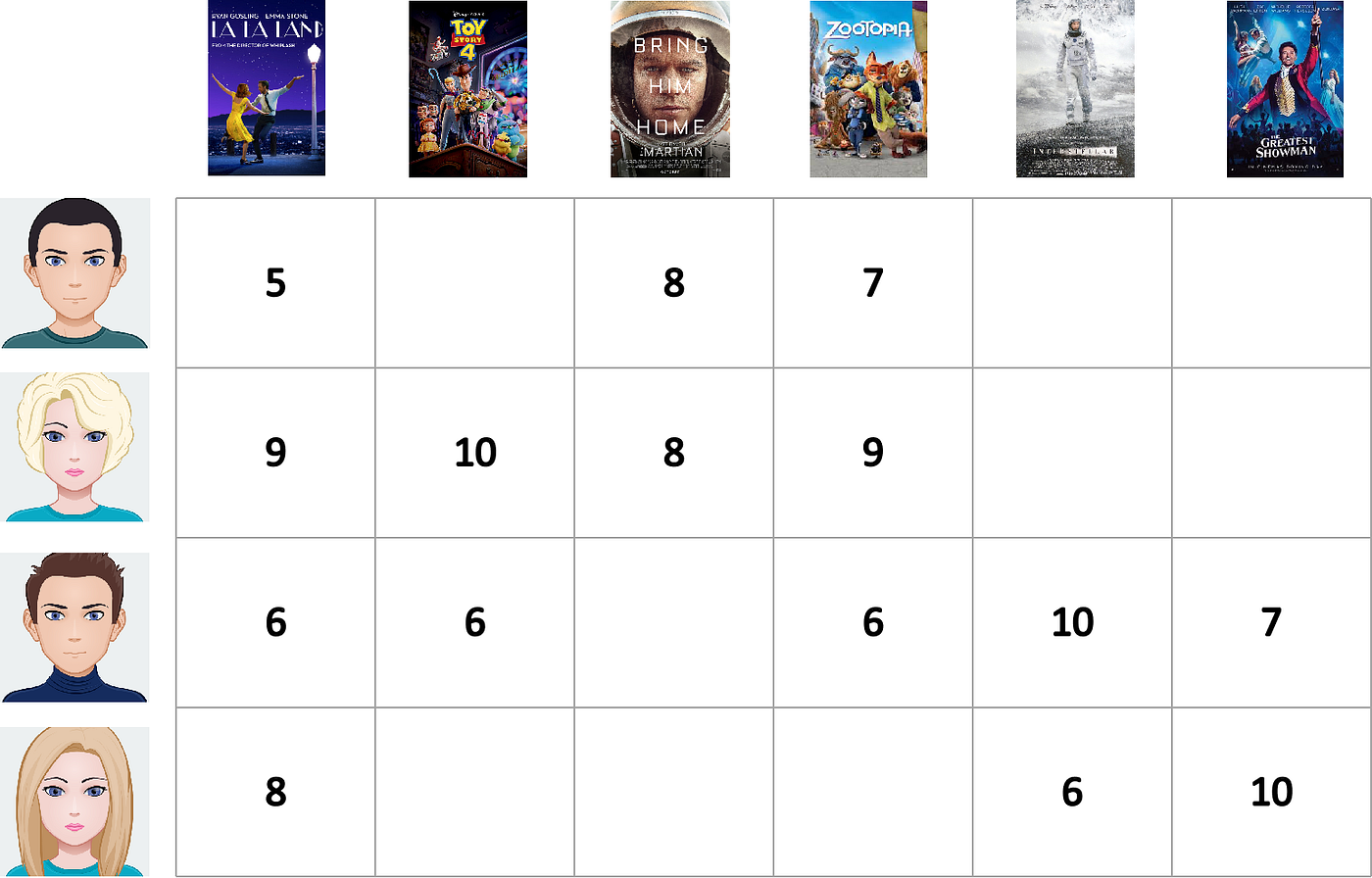 |
| Example of the user-item rating matrix |
Then, we can compare user or item vectors with a similarity metric to get a similarity score. For the user-based method, we can find the nearest user with the highest similarity score and feed that user's interest. For the item-based method, we can find the nearest item to the past rated items by a user.
3. Symbols and Notations Declaration
In this section, I will define some symbols and notations used in mathmatical representations.
The upper bold letters are used to represent matrics or sets(e.g., R: User-item rating matrix; U: A set of users in the database) The lower bold letters are used to represent vectors (e.g., u: A user vector)
4. Common Similariy Measurements
The table below lists the common similarity measurements:
| Similarity Name | Experssion |
| Non-normalized Cosine | \(cos(a,b)=\frac{a * b}{||a|| * ||b||}\) |
| Jaccard Similarity | \(JC(i,j)=\frac{|N(i) \cup N(j)|}{\sqrt{|N(i)||N(j)|}}\) | ItemIUF (Item Inverse-User Frequency) | \(ItemIUF(i,j)=\frac{\sum_{u \in N(i) \cup N(j) }{\frac{1}{log(1+|N(u)|)}}}{\sqrt{|N(i)||N(j)|}}\) | </tr>
Non-normalized Cosine and Jaccard Similarity are the most common ways to measure the similarity between two vectors. Item Inverse-User Frequency inferences from the theory of Term-frequency Inverse Document Frequency (TF-IDF). In this formula, N(x) represents the number of users rated by the item (x). Both measurements can be conducted in either a user-based or item-based way. Both measurements will give accurate similarity scores between two vectors.
5. Recommendation strategy
I can get a symmetric similarity matrix (W) after comparing all pairs of users or items. This matrix is usually called user-model (user-based CF) or item-model (item-based CF). I will use the item-model as an example to show how to generate the recommendation result for a user (u).
\[P_{u,j}={\sum}_{i \in N(u) \cap S(j,K)}{W_{j,i}r_{u,i}}\]In the formula above, \(P_{u,j}\) represents the prediction score of item (j) given by the user (u). This formula shows the weighted sum of the similarities and ratings among top-K most similar items for the user (u). In some cases, I need to try different neighbour-size (K) to verify the recommendation result to get the optimal one.
6. Discussion
User-based or item-based collaborative filtering provides an effective and straightforward way to compute the recommendations. However, it suffers from the issues of data sparsity. For example, given an item, I need to compare the similarities with all items in the database. Assuming that the database consists of millions of items, the execution will be very time-consuming. In addition, the items with lower similarity scores will mislead the recommendation results. Therefore, some low-rated items need to be dropped off to reduce the number of neighbours.