1. Graphs & Link Prediction

In recent years, with the popularity of deep learning, several researchers have migrated neural networks to recommendation tasks. Admittedly, some models have achieved significant improvements in performance compared to the performance of the traditional collaborative filtering algorithms. However, the problem that too long training time and complex model parameters increase the risk of over-fitting has aroused public attention.

A graph is a topological data structure consisting of nodes and edges, where nodes are events or objects, and edges are the relations between a pair of nodes [ref]. This thesis declares some notations and symbols. A bold-font upper letter represents a matrix (e.g., R), a graph (e.g., G) or a set (e.g., V), and a bold-font lower letter represents a vector (e.g., r).

Formula 1.1 below gives the mathematical definition of a graph. A graph is denoted as (G), which is a collection of vertices set (V) and edges set (E). Formula 1.2 defines the adjacent matrix (W) of G. The adjacent matrix is a symmetrical matrix where each entry indicates if there exists an edge between two nodes.

Alternatively, a recommendation task can be viewed as a link prediction problem. In graph theory, link prediction [ref] is such a technique that predicts if there exists a link between a pair of nodes. For a recommendation task, a standard recommendation dataset is viewed as a bipartite graph where nodes are the users and items and links are their interactions like ratings. Figure 1 (a) below illustrates the user-item rating graph, and Figure 1 (b) is the adjacent matrix of the graph, respectively.

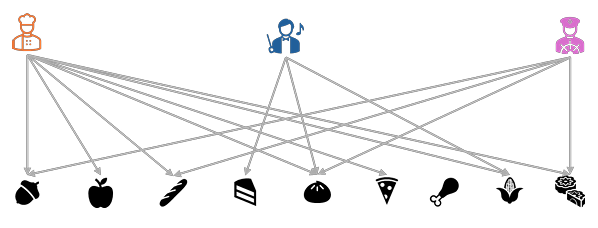(a) User-item bipartite graph
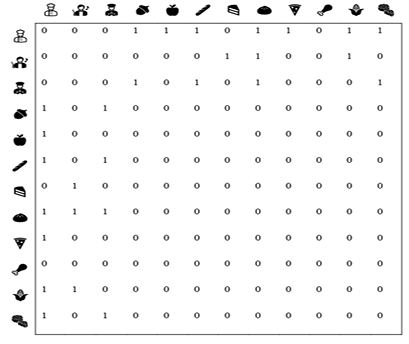(b) Adjacent Matrix (W)
Figure 1: User-item bipartite graph and adjacent matrix

2. Graph Models

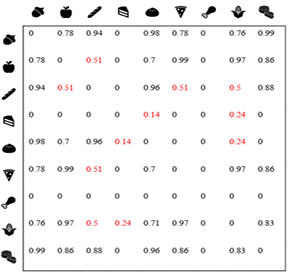
An inter-item interaction matrix is constructed from the user-item interaction matrix to measure the similarity between pairs of items for a neighbourhood-based collaborative method. Alternatively, an inter-item graph can be constructed from the inter-item matrix as the adjacent matrix. The nodes within the inter-item graph are the items, and the links are their similarity scores. The ways of constructing an inter-item graph are diverse, including memory-based similarity measures such as Cosine and Pearson and extraction from model-based methods like PureSVD latent factors. Figure 2 (a) and (b) show the inter-item matrix and graph constructed by the Cosine similarity measure. The inter-item graph is an undirected graph where the similarity scores are the same between a pair of nodes.

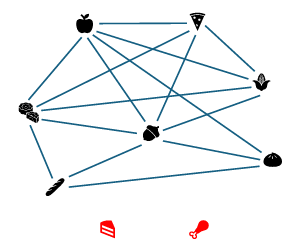(a) Inter-item adjacent matrix (b) Inter-item graph
Figure 2: Inter-item adjacent matrix and graph representation

We set a threshold to filter out the links whose weights are less than 0.7 and keep only the highly correlated links. Two outliers are within the graph, marked as the red items in Figure 2(b).