4.3 Shape Detection Algorithms

When I finished all of those preprocess procedures, the most significant part is to introduce the implementation of algorithm of each shape detection. In this section, Iwould introduce some basic techniques about how to detect different types of shapes.

4.3.1 Triangle

As we all knew, triangle is the simplest polygon. These are some basic concepts and classification in terms of triangle in table 4.3.1:

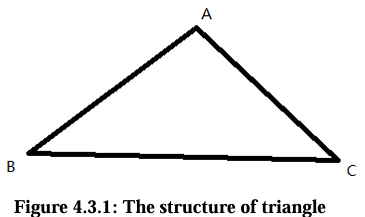
Triangle: A triangle is a polygon which is made up of three edges and three vertices (cf. Figure 4.3.1). If a triangle has three vertices, A, B and C, this triangle could bedenoted as △ABC. The length of side from vertex A to B is marked as AB.
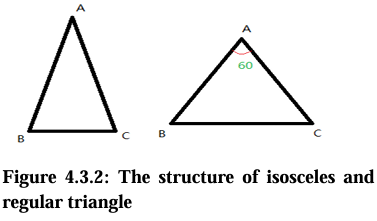
Isosceles Triangle: If there are two adjacent slides are equivalent in the length, this tringle is called as isosceles triangle (cf. Figure 4.3.2). Regular Triangle: Based on isosceles triangle, if there is an angle is 60 it is called as standard or regular triangle further (cf. Figure 4.3.2).
Table 4.3.1

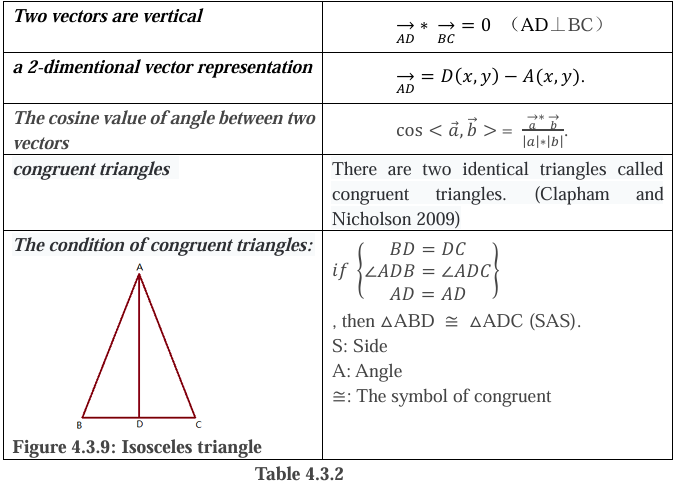
The table 4.3.2 shows some terms about the calculation of vectors and congruent triangle theorem:

p[0]=this->getAfterApproPoly()[0];
p[1]=this->getAfterApproPoly()[1];
p[2]=this->getAfterApproPoly()[2];
}

Point2d vec1,vec2;
double result, v1, v2, theta;

vec1.x=p[2].x-p[1].x;
vec1.y=p[2].y-p[1].y;

mid.x=(p[2].x+p[1].x)/2;
mid.y=(p[2].y+p[1].y)/2;

vec2.x=p[0].x-mid.x;
vec2.y=p[0].y-mid.y;

v1=sqrt(pow(vec1.x,2)+pow(vec1.y,2))
v2=sqrt(pow(vec2.x,2)+pow(vec2.y,2))

result=(vec1.x*vec2.x+vec1.y*vec2.y)/(v1*v2);
theta=acos(result)*(180/PI);
if (theta>=85 && theta <=95)
  judge[m]=true;

temp=p[1];
p[1]=p[0];
p[0]=p[2];
p[2]=temp;  //Change the order of nodes

m++
Code Segment: The implementation of Isosceles triangle

After ApproxPoly step, I get a vector with 3 points, and assigned them as p [0], p [1] and p [2] as shown in figure 4.3.4 (a). And then, I need to apply the condition of isosceles triangle. In fact, for an isosceles triangle, there are lots of conditions of judgement. In this case, I introduced a mathematical method based on vectors to prove an isosceles triangle. For example, if there is a triangle △ABC and AB = AC. I pick up the middle point of BC side as D. Thus, I could get BD=DC. In fact, why not prove the AB and AC side are equivalent in length directly? The reason is that I have to use endurance distance to calculate the distance between two points, and it might cause the complicated calculation of square and sqrt. But the mathematical vector would help me to reduce the complicated calculation instead of square and sqrt.

Further, if there is an angle between any adjacent sides of an isosceles triangle is equivalent to 60 degree, this triangle is considered as a standard or regular triangle. The picture 4.3.6 depicts the result of detection of Isosceles and regular Triangle.

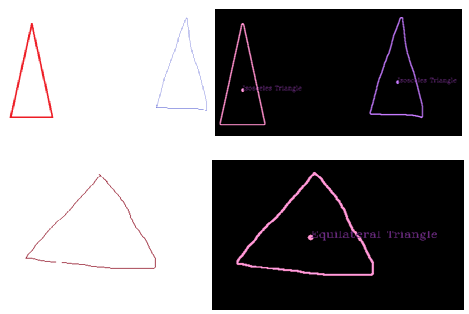
Figure 4.3.6: The detection result of isosceles and regular triangle