Object Shape Detection - Part 9: Finding Center of Contours

4.2.2 Center Finding

When all of the contours were found, the next step is to calculate the center point or particle of a contour. Moment is tool to describe the feature of image which has been used in several areas of computing, such as Image recognition, feature matching, image rebuilding and numeric compressing. (Wikipedia 2018).

The nature of moment is mathematical expectation. The normal formula of mathematical expectation is expressed as E(x) = ∫𝑥 ∗ 𝑓(𝑥) 𝑑𝑥. In this formula, f(x) refers to theprobability density of x. When it comes to computing graphics process, any gray image could be regarded as a flat object because that image has been processed from three or more channels to single channel. The pixel value of each cell could be seemed as the density of that point. Sometimes people want to figure out the mathematical expectation of one point to represent the Image Moment at that point. For the image moment, it could be classified as zero, first and second order. The zero (1) or first (2) order moment could be used to calculate the center or gravity of a shape, and second (3) order moment is mainly applied to calculate the direction of a shape. In these three formulas, (i, j) are one element of contours vector.

Therefore, the coordinate of center of gravity could be expressed as \( x = \frac{𝑀10}{M00}, Y = \frac{M01}{M00}\) of one contour.

The code segment A is the illustration of calculation of coordinate center point of a contour. In my project, the center point is very significant to the detection of circle and ellipse. The figure 4.2.8 shows the center of each contour.

Point Controller::calculate_center_moment(vector<Point> c)
{
    Moments mo=moments(c,false);
    Point2f acenter(mo.m10/mo.m00,mo.m01/mo.m00);
    return acenter;
}

Figure 4.2.8 (a): The Original Image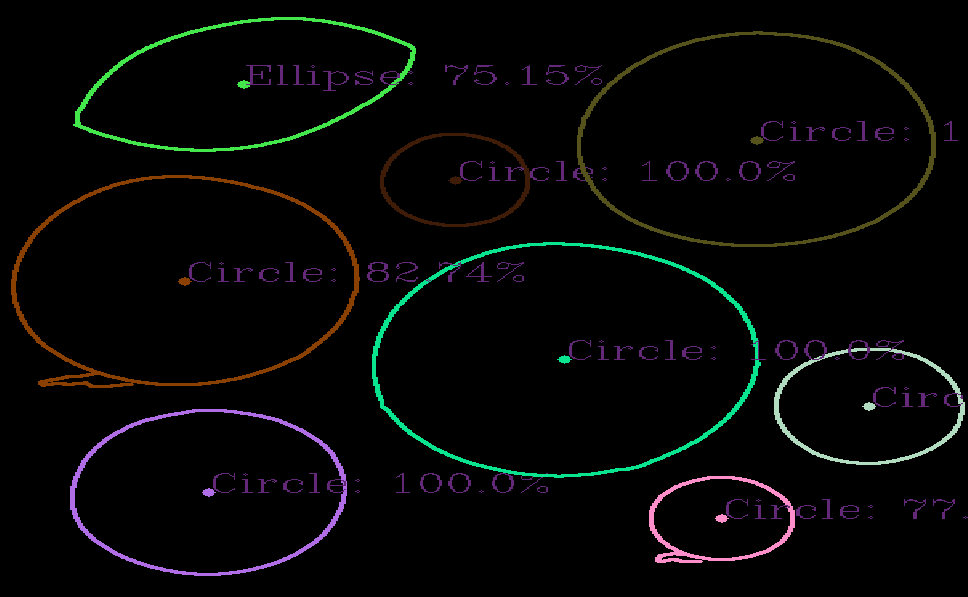

Figure 4.2.8 (b): The Coordinate of center of each contour